EM算法

本文主要基于Andrew Ng的Lecture Notes(下载原文)，附加一些我个人的总结和理解。

EM全称Expectation Maximization，翻译成最大化期望算法，是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量（Latent Variable）

由于hexo对latex支持不是很好，我先在本地写好，截图贴上来非常方便，不用再担心渲染出问题。

1. Jensen不等式

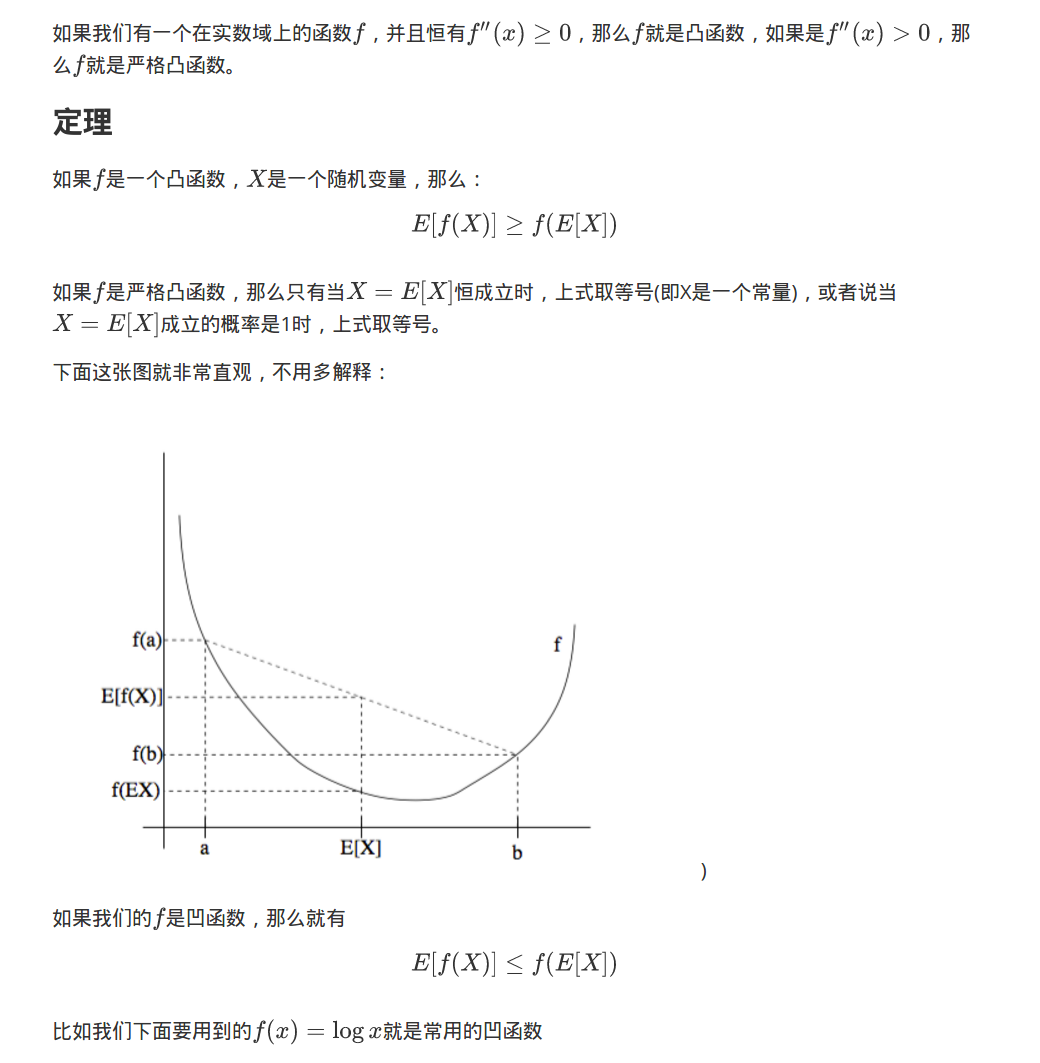
2. EM算法

3. 收敛性

4. 总结

EM是一个在已知部分相关变量的情况下，估计未知变量的迭代技术。

最大期望演算法在统计中被用于寻找，依赖于不可观察的隐性变量的概率模型中，参数的最大似然估计。上面的样本x是可以观察到的不完整的值，但是z是不能观察到的，如果z是已知的话，那就不需要EM算法了，直接求最大化似然函数的模型参数即可，我们这里指x是不完整的就是说缺少z，引入这个隐含变量可以将问题简化，而我们利用Jensen不等式还有一个原因是一开始是log里面求和，显然是比较难优化的，而利用Jensen不等式将求和放到了外面，计算起来就方便多了。