C++实现代码的error和论文一致(最近又新添加了一个example，重写了一些代码)，详见我的github链接
以下是论文解读：效果见最后

1.Framework

整个流程基于Cascade Pose Regression(CVPR 2010)，分为T个stage，在训练时步骤如下（testing也类似）

1. 每个stage先抽取local binary features，
2. 然后根据真实的$\varDelta {\hat{S}}_i$ 用linear regression训练一个regressor，
3. 最后用训练出来的regressor得到$\varDelta S_i$(是$\varDelta {\hat{S}}_i$的近似)去更新前一个stage的shape，得到更加精确的shape

1.1 Training Phase:

Input: Image set {$I$}(N samples), ground truth shapes {$\hat{S}$}, initial shapes set {$S^0$}
For t=1:T do
        $features_i = \phi^t (I_i,S_i^{t-1})$
        $\varDelta \hat{S_i}=\hat{S_i} - S^{i-1}$
        $E=\sum {\lVert \hat{S_i} - R^t(features_i)\rVert}^2$
        $\varDelta S_i=R^t(features_i)$
        $S^t_i=S^{t-1}_i+\varDelta S_i$
End For

1.2 Testing phase

Input: Image I, initial shape $S^0$
Output: refined shape $S$
For t=1:T do #总共有T个stage
        $features = \phi^t(I,S^{t-1})$
        $\varDelta S=R^t(features)$
        $S^t=S^{t-1}+\varDelta S$
End For

2. 抽取Local Binary Features

1. 先random产生500个pixel difference features
2. 选取最具有分辨力的pixel difference features作为Random Forest中每棵树中的非叶子结点
3. 输入图片得到Local Binary Features

2.1 Pixel Difference Features

Pixel Difference Features源自CVPR 2012的一篇叫face alignment by explicity shape regression的文章。

1. Pixel Indexed Features
   
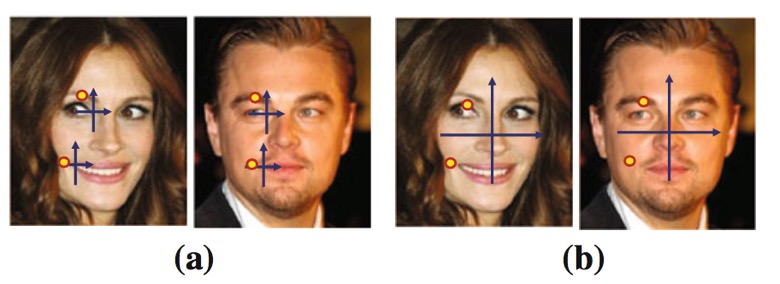
   如上图，作者认为对于特定的一个landmrk，它周围的有些点是几何不变的，比如我们有一个landmark是左眼的右眼角$P(x,y)$，在它的上方某个地方$\varDelta P(\varDelta x, \varDelta y)$具有不变的性质,比如附近的眉毛某点 $P(x+\varDelta x, y+\varDelta y)$ 就是黑色的,这个对每个人来说都是一样，当然由于光照等其他因素的原因，这个颜色还是有很大差异的，那么作者就提出了 Pixel Difference Features
2. Pixel Difference Features
   其实很简单，就是将附近某两个点的值相减得到一个差值，而这个值很大程度上在一个阈值内浮动，而且还可以剔除光照等因素的影响，即
   $$feature = I(x+\varDelta x_1, y+\varDelta y_1)-I(x+\varDelta x_2, y+\varDelta y_2)$$

2.2 创建Random Forest

Random Forest维基链接。Random Forest由很多tree组成，相比于单棵tree能够防止模型的over fitting。Random Forest能用于regression(本文用到的功能)和classification。
那么如何建立Random Forest，主要是如何选择split node，下面以如何构建一颗regression tree为例。

1. 首先我们确定一个landmark l，随机产生在l附近的500个pixel difference features的位置，然后对training中的所有images抽取这500个features，
2. 确定要构建l的第几个棵树（其他树一样，只是训练数据不一样而已）
3. 从树根节点开始
   var = variance of landmark l of traing images,
   var_red = -INFINITY, fea = -1, left_child = NULL, right_child = NULL
   For each feature f:
           threshold = random choose from all images’s feature f
           // 比如现在所有图的f的值是2，2，2，4，5，3（假设有5张图），那么随机选择threshold可能是3
           tmp_left_child = images with f < threshold
           // 左子节点为所有f小于threshold的图片
           tmp_right_child = images with f >= threshold
           tmp_var_red = var - |left_child|/|root|*var_tmp_left_child - |right_child|/|root|*var_tmp_right_child
           // var_tmp_left_child是左子节点landmark l的variance
           if ( tmp_var_red > var_red) {
                   mvar_red = tmp_var_red
                   fea = f
                   left_child = tmp_left_child
                   right_child = tmp_right_child
           }
   End For
   实际上var是固定的，所以不用算，|left_child|是当前left_child所包含的图片数，|root|表示root包含的图片数，实际计算的时候可以省去，因为是定的。
   fea就是最后选择的feature
4. 对子节点left_child和right_child做跟3一样的操作，直到达到tree的最大depth，或者对于某一个根节点根据maximum variance reduction找到的feature是恰好一个child包含了所有的图，而另一个child没有图（事实上这个情况基本上不太可能出现），所以训练的时候基本上能够达到定义的max_depth，经我个人验证max_depth=5,6就可以了，在深很容易出现overfitting的问题
5. landmark l的其他树也一样如上，对其他landmark和对l的操作一样

2.3 Local Binary Features

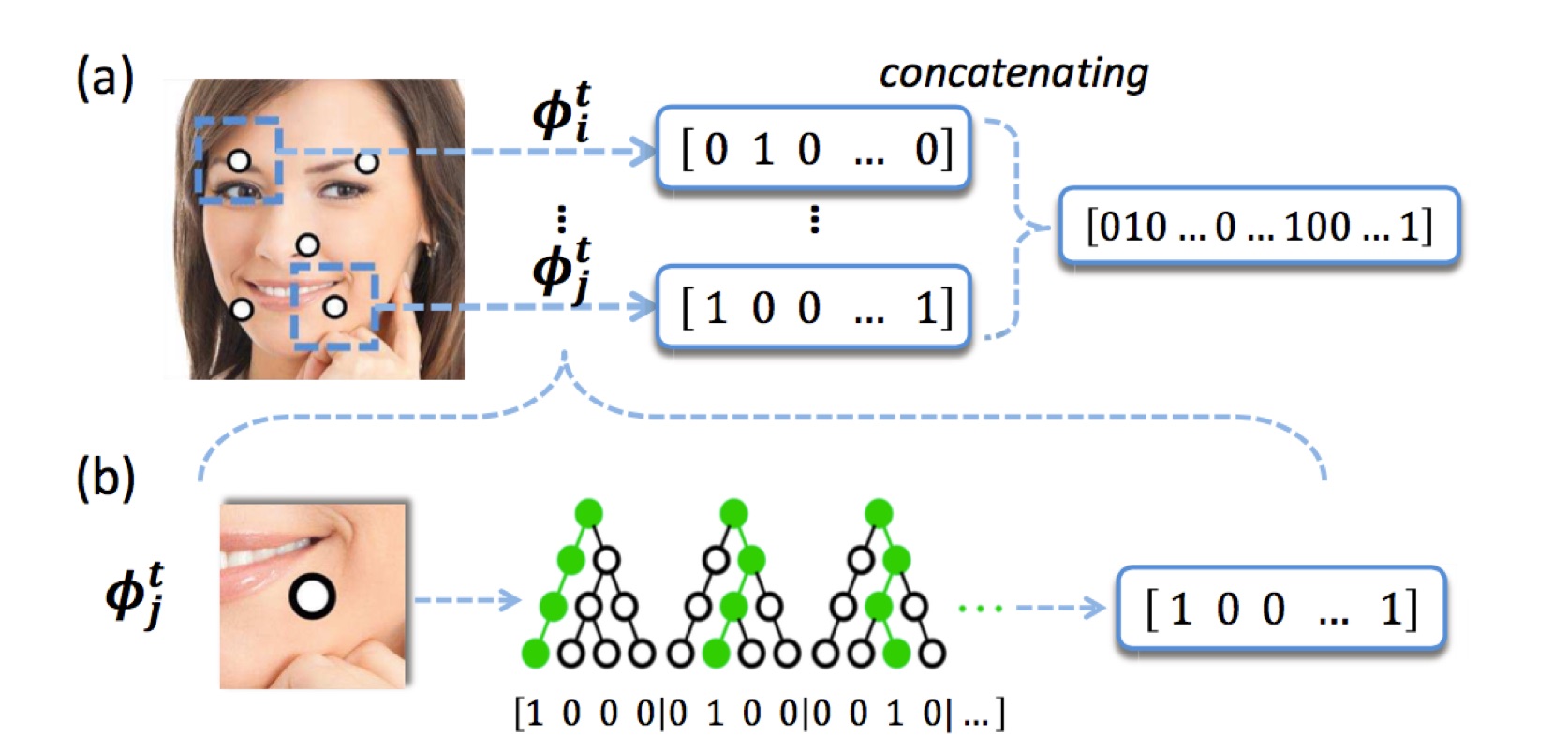
那么对于每一张图的每一个landmark的每一棵树最后都会输出一个值，如上图下方，第一棵树遍历后来到了最左边的子节点所以记为[1, 0, 0, 0]，对于每一棵树访问到的叶子节点记为1，其他的记为0，然后一个landmark拥有一个forest即有多棵树，那么把所有的结果连起来就是$\phi_l^t=[1,0,0,0,0,1,0,0,0,0,1,0,…]$，真正的Local Binary Features是将所有的landmark的这些feature都连起来。
$$\phi^t = [\phi_1^t, \phi_2^t,…,\phi_L^t]$$
所以我们可以看出这是一个很稀疏的向量，中间为1的个数是所有landmark中tree的总个数，其余的为0。然后就是要训练一个global linear regression了

3. Learning Global Linear Regression

对每一个landmark训练时用的都是同一个local binary features.

1. 比如对于第一个landmark的$\varDelta x$坐标进行regression，输入就是所有图片的local binary feature矩阵，所有$\varDelta x$坐标组成的vector作为regression target，最后可以得到一个权重向量w，然后有了新的图片，抽取它的local binary feature后，乘以w就可以得到预测的$\varDelta x$值，最后加到上一个stage的$x$上面得到新的$x$
2. 对于第一个landmark的$\varDelta y$也是一样，这里的local binary feature矩阵和上面$\varDelta x$矩阵的一样，只是要regression的target $\varDelta y$不一样，
3. 其他的landmark同上
4. 上面的公式，是将所有的landmark的w都合在一起了，求一个整体的W

4. 效果如图：还是很不错的

initial shape

final shape